Curiosidade: Números Triangulares | a forma escondida dos naturais
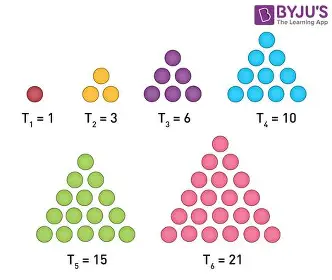
Os números naturais guardam padrões surpreendentes. Uma curiosidade simples e elegante são os números triangulares: 1, 3, 6, 10, 15… , cada termo conta pontos que formam um triângulo equilátero. A fórmula fechada permite calcular o n-ésimo número triangular rapidamente.
Definição: o n-ésimo número triangular T(n) é a soma dos n primeiros naturais:
T(n) = 1 + 2 + 3 + … + n = n × (n + 1) / 2
Curiosidade histórica: Diz-se que Gauss, ainda criança, usou essa soma rápida para calcular somas aritméticas na escola — ele percebeu o pareamento 1+n, 2+(n−1), … que leva à fórmula acima.
Exemplo prático: número de apertos de mão numa reunião com n pessoas (assumindo apertos distintos por par) = T(n−1).
Quer ver? Insere um número natural e a visualização abaixo mostra T(n) como pontos e calcula o valor exato.
Visualização
Cada bloco azul representa um ponto; organizei-os em linhas para lembrar um triângulo.
Conclusão: os números naturais não são apenas contagem , são padrões. Os números triangulares mostram como estruturas simples (soma dos naturais) se traduzem em formas geométricas, fórmulas fechadas e aplicações práticas.







